Question

Part complete Horizontally-polarized light passes through a polarizing sheet, and only 25 % of the intensity of the incident light is transmitted through the sheet. What angle does the polarization of the light make with the horizontal after passing through the polarizer?

Answer 1

60°

Step-by-step explanation:

I₀ = Intensity of unpolarized light

θ = Angle between the axis of the filter and polarization direction

Intensity of polarzied light

`I=I_0cos\theta`

Here, the light that is transmitted is reduced by 25% that means

`I=0.25I_0`

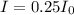
So,

`0.25I_0=I_0cos^2\theta\\\Rightarrow cos^2\theta =0.25\\\Rightarrow cos\theta =5\\\Rightarrow \theta= cos^(-1)0.5\\\Rightarrow \theta=60^(\circ)`

∴ The angle between the axes of the polarizer and the analyzer is 60°