Question

Suppose that an Egyptian farmer claims to have discovered a linen burial cloth used during Egypt's Middle Kingdom some 4000 years ago. Careful analysis shows that the cloth contains 80% of the 14C that it is estimated to have originally contained. How old is the cloth?

Answer 1

1844 years

Step-by-step explanation:

¹⁴C follows a first-order beta-decay according to the following equation.

¹⁴C ⇒ ¹⁴N + β⁻

We can calculate the concentration of ¹⁴C after some time using the following expression.

`ln(([C]_(t))/([C]_(0)) )=-k.t`

where,

[C]t is the concentration of ¹⁴C after some time

[C]₀ is the original concentration of ¹⁴C

k is the rate constant

t is the time elapsed

We can calculate the rate constant if we know the half-life (t1/2) using the following expression.

`k=(ln2)/(t_(1/2))`

Half-life of ¹⁴C is 5730 years. Then,

`k=(ln2)/(5730y)=1.210* 10^(-4) y^(-1)`

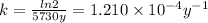
The elapsed time when the concentration of ¹⁴C is 80% of original is:

`ln((0.8[C]_(0))/([C]_(0)) )=-1.210* 10^(-4) y^(-1) * t\\t = 1844y`