Answer:
time of flight T= 5.77sec
maxiumum height h max= 66.78m
horizontal range S=50.91m
Step-by-step explanation:
Assume that the footaball moves with the initial velocity= Vo=40m/s
and angle
 =
=
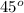 (for maximum range)
(for maximum range)
Given that,
the distance from place of attempting goal to goal post =d= 36.58m
height of goal post=3.084m
For projectile motion, time of flight T is,
T=
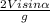 =
=
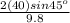
T= 5.77sec
According to second equation of motion
S=Vot+ 1/2 gt^2
S= h max, Vo= vertical component of velocity= 40sin 45=28.28
t=average time= (time of flight +0 )/2= 3.6/2=1.8sec
h max= 28.28*1.8+ 1/2(9.8)(1.8)^2
h max= 66.78m
For horizontal range,
S= v*t
v= horizontal component of velocity= Vocos45=40cos 45 = 28.28
t=average time= (time of flight +0 )/2= 3.6/2=1.8sec
S= 28.28*1.8
S=50.91m