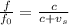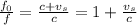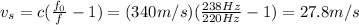Answer:
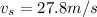
Step-by-step explanation:
If the person hearing the sound is at rest, then the equation for the frequency heard
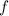 given the emitted frequency
given the emitted frequency
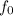 , the speed of the truck
, the speed of the truck
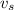 and the speed of sound
and the speed of sound
 will be:
will be:
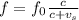
Where
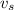 will be positive if the truck is moving away from the person, and negative otherwise. We then do:
will be positive if the truck is moving away from the person, and negative otherwise. We then do: