Question

Sec squared 55 - tan squared 55

Answer 1

sec squared 55 – tan squared 55 = 1

Step-by-step explanation:

Given, sec square 55 – tan squared 55

We know that,

`\sec \Theta=\frac{\text {hypotenuse}}{\text {base}}`

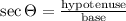
And,

`\tan \theta=\frac{\text { perpendicular }}{\text { base }}`

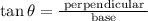
where Ө is the angle

Substituting the values

`\left(\frac{\text {hypotenuse}}{\text {base}}\right)^(2)-\left(\frac{\text { perpendicular }}{\text {base}}\right)^(2)`

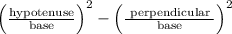
Solving,

`\frac{(\text {hypotenuse})^(2)-(\text {perpendicular})^(2)}{(\text {base}) *(\text {base})}`

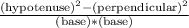
According to Pythagoras theorem,

`\text { (hypotenuse) }^(2)-\text { (perpendicular) }^(2)=(\text { base })^(2)`

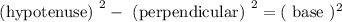
Putting this in the equation;

squared 55 - tan squared 55 =

`\frac{(\text {hypotenuse})^(2)-(\text {perpendicular})^(2)}{(\text {base}) *(\text {base})}=\frac{(\text {base})^(2)}{(\text {base}) *(\text {base})}=1`

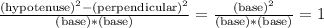
Therefore, sec squared 55 – tan squared 55 = 1