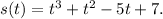Question

A particle moves in a straight line and has acceleration given by a(t) = 6t + 2. Its initial velocity is v(0) = −5 cm/s and its initial displacement is s(0) = 7 cm. Find its position function, s(t). SOLUTION Since v'(t) = a(t) = 6t + 2, antidifferentiation gives

Answer 1

Answer: The required position function is
`s(t)=t^3+t^2-5t+7.`

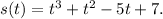
Step-by-step explanation: Given that a particle moves in a straight line and has acceleration given by

`a(t)=6t+2.`

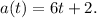
The initial velocity of the particle is v(0) = −5 cm/s and its initial displacement is s(0) = 7 cm.

We are to find the position function s(t).

We know that the acceleration function a(t) is the derivative of the velocity function v(t). So,

`v^\prime(t)=a(t)\\\\\Rightarrow v^\prime(t)=6t+2\\\\\Rightarrow v(t)=\int (6t+2) dt\\\\ \Rightarrow v(t)=3t^2+2t+A~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

Also, the velocity function v(t) is the derivative of the position function s(t). So,

`s^\prime(t)=v(t)\\\\\Rightarrow s^\prime(t)=3t^2+2t+A\\\\\Rightarrow s(t)=\int(3t^2+2t+A) dt \\\\\Rightarrow s(t)=t^3+t^2+At+B~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

From equation (i), we get

`v(0)=0+0+A\\\\\Rightarrow A=-5,~\textup{where A is a constant}`

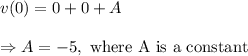
and from equation (ii), we get

`s(0)=0+0+0+B\\\\\Rightarrow B=7,~\textup{where B is a constant}.`

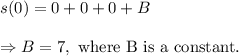
Substituting the values of A and B in equation (ii), we get

`s(t)=t^3+t^2-5t+7.`

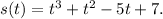
Thus, the required position function is
`s(t)=t^3+t^2-5t+7.`