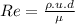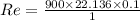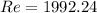Question

Calculate the Reynolds number for an oil gusher that shoots crude oil 25.0 m into the air through a pipe with a 0.100-m diameter. The vertical pipe is 50 m long. Take the density of the oil to be 900 kg/m3 and its viscosity to be 1.00 (N/m2)·s (or 1.00 Pa·s).

Answer 1

`Re=1992.24`

Step-by-step explanation:

Given:

vertical height of oil coming out of pipe,
`h=25\ m`

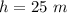
diameter of pipe,
`d=0.1\ m`

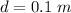
length of pipe,
`l=50\ m`

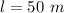
density of oil,
`\rho = 900\ kg.m^(-3)`

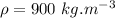
viscosity of oil,
`\mu=1\ Pa.s`

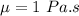
Now, since the oil is being shot verically upwards it will have some initial velocity and will have zero final velocity at the top.

Using the equation of motion:

`v^2=u^2-2gh`

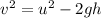
where:

v = final velocity

u = initial velocity

Putting the respective values:

`0^2=u^2-2* 9.8* 25`

`u=22.136\ m.s^(-1)`

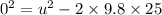
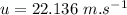
For Reynold's no. we have the relation as:

`Re=(\rho.u.d)/(\mu)`

`Re=(900* 22.136* 0.1)/(1)`

`Re=1992.24`