Question

If
`x-12√(x) +36=0`, what is the value of x?

A.
`6`

B.
`6^(2)`

C.
`6^(3)`

D.
`6^(4)`

Answer 1

x = 36

Explanation:

`x - 12√(x) + 36 = 0`

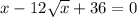
Subtract x and 36 from both sides.

`-12√(x) = -x - 36`

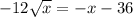
Divide both sides by -1.

`12√(x) = x + 36`

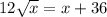
Square both sides.

`144x = x^2 + 72x + 1296`

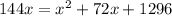
Subtract 144x from both sides.

`0 = x^2 - 72x + 1296`

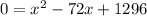
Factor the right side.

`0 = (x - 36)^2`

`x - 36 = 0`

`x = 36`

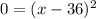
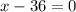
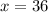
Since the solution of the equation involved squaring both sides, we musty check the answer for possible extraneous solutions.

Check x = 36:

`x - 12√(x) + 36 = 0`

`36 - 12√(36) + 36 = 0`

`36 - 12* 6 + 36 = 0`

`36 - 72 + 36 = 0`

`0 = 0`

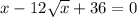
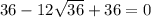
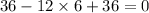
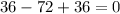
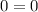
Since 0 = 0 is a true statement, the solution x = 36 is a valid solution.