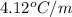Question

The normal freezing point of a certain liquid

X

is

0.4°C

, but when

5.90g

of urea

NH22CO

are dissolved in

450.g

of

X

, it is found that the solution freezes at

−0.5°C

instead. Use this information to calculate the molal freezing point depression constant

Kf

of

X

Answer 1

Answer : The molal freezing point depression constant of X is
`4.12^oC/m`

Explanation : Given,

Mass of urea (solute) = 5.90 g

Mass of X liquid (solvent) = 450.0 g

Molar mass of urea = 60 g/mole

Formula used :

`\Delta T_f=i* K_f* m\\\\T^o-T_s=i* K_f*\frac{\text{Mass of urea}* 1000}{\text{Molar mass of urea}* \text{Mass of X liquid}}`

where,

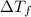`\Delta T_f` = change in freezing point

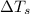`\Delta T_s` = freezing point of solution =
`-0.5^oC`

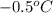
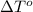`\Delta T^o` = freezing point of liquid X=
`0.4^oC`

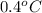
i = Van't Hoff factor = 1 (for non-electrolyte)

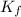`K_f` = molal freezing point depression constant of X = ?

m = molality

Now put all the given values in this formula, we get

`[0.4-(-0.5)]^oC=1* k_f* (5.90g* 1000)/(60g/mol* 450.0g)`

`k_f=4.12^oC/m`

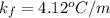
Therefore, the molal freezing point depression constant of X is
`4.12^oC/m`