Answer:
-0.750
Explanation:
A lumber company is making boards that are 2867.0 millimeters tall.
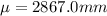
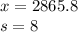
A level of significance of 0.05
Sample size = n = 25
Since n < 30
So we will use t test
Formula :
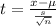
Substitute the values in the formula :
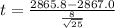
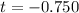
Hence the value of the test statistic is -0.750