Answer:
a)a= 4.62 m/s²
b)μ = 0.462
Step-by-step explanation:
Given that
m= 1200 kg
r = 70 m
v= 18 m/s
a)
Centripetal acceleration ,a
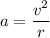
By putting the values
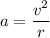
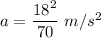
a= 4.62 m/s²
b)
To keep the car from slipping ,the radial force should be equal to the friction force
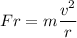
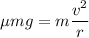
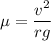
By putting the values
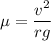
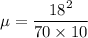 ( take g =10 m/s²)
( take g =10 m/s²)
μ = 0.462