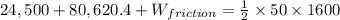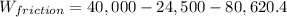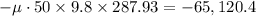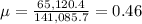Question

Kieran takes off from rest down a 50 m high, 10° slope on his jet-powered skis. The skis have a thrust of 280 N parallel to the surface of the slope. The combined mass of skis and Kieran is 50 kg (the fuel mass is negligible). Kieran's speed at the bottom is 40 m/s. What is the coefficient of kinetic friction of his skis on snow?

Answer 1

Answer:0.46

Step-by-step explanation:

Given

Initial height
`h=50 m`

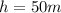
inclination
`\theta =10^(\circ)`

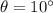
Thrust
`=280 N`

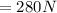
combined mass of kieran and skis
`m=50 kg`

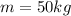
Speed at the bottom
`v=40 m/s`

From Work Energy Theorem

Work done by all the force is equal to change in kinetic Energy

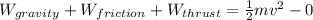`W_(gravity)+W_(friction)+W_(thrust)=(1)/(2)mv^2-0`------------1

distance traveled along the slope
`x=(50)/(\sin 10)=287.93 m`

`W_(gravity)=mgh=50* 9.8* 50=24500 J`

`W_(thrust)=F* x=280* 287.93=80,620.4 J`

`W_(friction)=-\mu mg\cos 10`

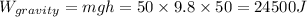
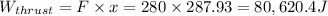
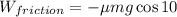
substitute in 1

`24,500+80,620.4+W_(friction)=(1)/(2)* 50* 1600`

`W_(friction)=40,000-24,500-80,620.4`

`-\mu \cdot 50* 9.8* 287.93=-65,120.4`

`\mu =(65,120.4)/(141,085.7)=0.46`