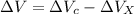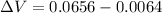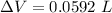Answer:
Step-by-step explanation:
Given:
- Initial temperature of the coolant,

- final temperature of the coolant,

- total volume of the coolant,
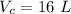
- coefficient of volume expansion for coolant,

- volume of Al radiator,
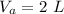
- volume of steel radiator,
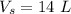
We have:
coefficient of volume expansion for Aluminium,

coefficient of volume expansion for steel,
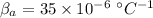
Now, change in volume of the coolant after temperature rises:
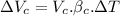

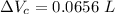
Now, volumetric expansion in Aluminium radiant:
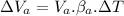

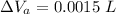
Now, volumetric expansion in steel radiant:
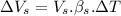
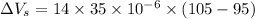
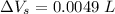
∴Total extra accommodation volume created after the expansion:

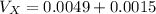
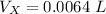
Hence, the volume that will overflow into the small reservoir will be the volume of coolant that will be extra after the expanded accommodation in the radiator.