Question

How much TV do college students watch? A survey of 361 students recorded the number of hours of television they watched per week. The sample mean was 6.504 hours with a standard deviation of 5.584. The standard error of the mean was 0.294. Find a 90% confidence interval for the population mean. Round your answer to three decimal places

Answer 1

Answer: 90% confidence interval would be (6.022,6.986).

Explanation:

Since we have given that

Number of students = 361

Sample mean = 6.504

Sample standard deviation = 5.584

Standard error of the mean = 0.294

At 90% confidence level,

So, α = 0.01

So, z = 1.64

Margin of error is given by

`z* \text{Standard error}\\\\=1.64* 0.294\\\\=0.48216`

So, Lower limit would be

`\bar{x}-0.482\\\\=6.504-0.482\\\\=6.022`

Upper limit would be

`\bar{x}+0.482\\\\=6.504+0.482\\\\=6.986`

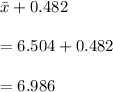
So, 90% confidence interval would be (6.022,6.986).