Question

I will give 100 points to whoever has the best answer

1. Seiji and Gavin both worked hard over the summer. Together they earned a total of $525. Gavin earned $25 more than Seiji.

(a) Write a system of equations for the situation. Use s for the amount Seiji earned and g for the amount Gavin earned.

(b) Graph the equations of the system on the graph

(c) Use your graph to estimate how much each person earned, and explain your results.

Answer 1

a)

`\left\{\begin{matrix}g=525-s\\ g=s+25\end{matrix}\right.`

c)

Gavin earned $275

Seiji earned $250

Explanation:

a) Denoting s as the earning of Seiji and g the earnings of Gavin, we know they together earned $525. This forms the equation

s+g=525, or equivalently

`g=525-s`

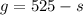
We also know that Gavin earned $25 more than Seiji. It can be written as

`g=s+25`

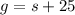
Combining both equations we get the system

`\left\{\begin{matrix}g=525-s\\ g=s+25\end{matrix}\right.`

b) The graph is shown below

c) Both functions have one point in common. It's the solution of the system. We can conclude that

Gavin earned $275

Seiji earned $250