Question

A 259-kV power transmission line carrying 429 A is hung from grounded metal towers by ceramic insulators, each having a 0.71×109 Ω resistance. What is the resistance to ground of 95 of these insulators? Give your answer in MΩ. (Please note that the ceramic insulators are like resistors that are connected in parallel.)

Answer 1

The resistance is
`7.47*10^(6)\ \Omega`.

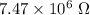Step-by-step explanation:

Given that,

Power = 259 kV

Current = 429 A

Resistance
`R=0.71*10^(9)\ Omega`

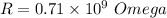
We need to calculate the current in each insulator

Using formula of current

`I=(P)/(R)`

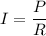
Put the value into the formula

`I=(259*10^(3))/(0.71*10^(9))`

`I=3.64*10^(-4)\ A`

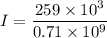
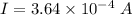
So all 95 insulators are in parallel

We need to calculate the resistance

Using formula of resistance

`(1)/(R)=\sum_(i=1)^(95)(1)/(R_(i))`

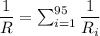
Put the value into the formula

`(1)/(R)=(95)/(0.71*10^(9))`

`(1)/(R)=1.338*10^(-7)`

`R=(1)/(1.338*10^(-7))`

`R=7473841.5=7.47*10^(6)\ \Omega`

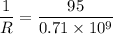
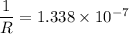
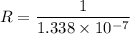
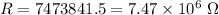
Hence, The resistance is
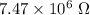`7.47*10^(6)\ \Omega`.