Question

A wire is bent to form a circular loop whose radius is 5 cm. The wire carries a current of 10.0 A. The resulting current loop is placed in a uniform magnetic field of 12 T, with its magnetic dipole moment vector making an angle of 30 degree with the direction of the field. Find the magnitude of the torque that the magnetic field exerts on the wire. 1.88 N.m 0.94 N.m 0.47 N.m 0.16 N.m 0.0 N.m

Answer 1

To solve this problem it is necessary to use the concepts related to Torque generated by the current.

From its definition as magnitude, it can be described as

`\tau = IAB sin\theta`

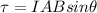
Where

A = Cross Sectional Area

I = Current

B = Magnetic Field

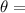`\theta =`Angle between the magnetic field lines and normal to the loop area

Our values are given as

`\theta = 30\°\\I = 10A\\A = \pi r^2 = \pi * (5*10^(-2)) ^2 \\A = 7.85*10^(-3)m^2\\B = 12T`

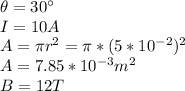
Replacing at the previous equation

`\tau = IAB sin\theta`

`\tau = (10)(7.85*10^(-3))(12) sin30`

`\tau =0.471 Nm`

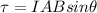
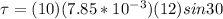
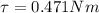
Therefore the correct answer is 0.47Nm.