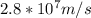Question

Two particles of equal masses (m=5.5x10-15 kg) are released from rest with a distance between them equal to 1 m. If particle A has a charge of 12 μC and particle B has a charge of 60 μC, what is the speed of particle B at the instant when the particles are 3m apart?

Answer 1

To solve this problem it is necessary to apply the law of conservation of Energy and the law of Coulomb.

This way we have to

`\Delta EE = \Delta KE`

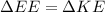
Where,

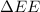`\Delta EE` = Potential Electric Energy

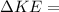`\Delta KE =` Kinetic Energy

Therefore,

`(kq_Aq_B)/(d)-(kq_Aq_B)/(d')= (1)/(2)mv^2+(1)/(2)mv^2`

`(kq_Aq_B)/(d) = (kq_Aq_B)/(d')+mv^2`

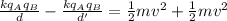
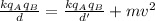
Replacing we have that

`((9*10^9)(12*10^(-6))(60*10^(-6)))/(1)=((9*10^9)(12*10^(-6))(60*10^(-6)))/(3)+5.5*10^(-15)v^2`

`5.5*10^(-15)*v^2 = ((9*10^9)(12*10^(-6))(60*10^(-6)))/(1)-((9*10^9)(12*10^(-6))(60*10^(-6)))/(3)`

`v = 2.8*10^7m/s`

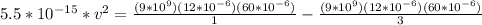
Therefore the speed of particle B at the instant is
`2.8*10^7m/s`