Answer:
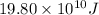
Step-by-step explanation:
Given
mass of satellite
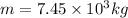
orbital radius
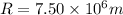
mass of Earth

Minimum amount of Energy to move Satellite from its orbit to an infinite distance is sum of Potential Energy + Kinetic Energy of Satellite
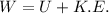
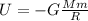
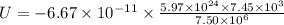
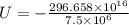
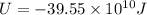
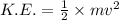
Where
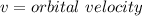
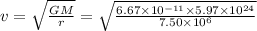
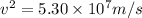
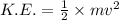
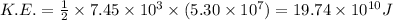
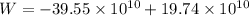
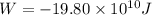
i.e.
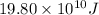 Energy is required to provide to move Satellite out of its orbit
Energy is required to provide to move Satellite out of its orbit