Question

A private tutoring company charges $20 for a 1-hour session. Currently, 300 students are each tutored for an hour each week. Since the company is losing money, the owner has decided to increase the price. For each 50¢ increase, she estimates that 5 fewer students will participate. If the company needs to bring in $6,240 per week to stay in business, what price must be charged for a 1-hour tutoring session to produce this amount of revenue?

Answer 1

$24 or $26

Explanation:

If for each 50¢ increase, the estimate is that 5 fewer students will participate, for each $1 increase, the estimate is that 10 fewer students will participate.

Revenue is the product of the amount charged per hour by the number of students tutored for an hour each week. The revenue function, R(x), written as a function of the amount increased per lesson in dollars,x, is given by:

`R(x) = (20+x)*(300 - 10x)\\`

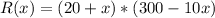
Since revenue needs to be $6,240 per week for the company to stay in business:

`6,240 = (20+x)*(300 - 10x)\\\\-10x^2 +100x+6,000-6,240=0\\x^2 -10x+24=0\\`

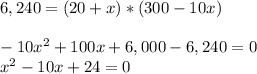
According to the sum & product of roots properties:

`x_(1) +x_(2) = -(-10)\\x_(1) x_(2)= 24\\x_(1) = 4\\x_(2) = 6`

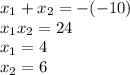
Therefore, either a $4.00 or a $6.00 increase would yield in a revenue of $6,240.

The price that must be charged for a 1-hour tutoring session is $24 or $26