To solve this problem it is necessary to apply the equations related to the law of Maus.
By the law of Maus we know that
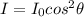
Where,
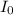 = Intesity of incident light
= Intesity of incident light
I = Intensity of polarized light
With our values we have that
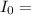 6V/m
6V/m
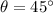
Then
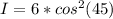
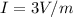
Therefore the maximum value of the transmitted E vector is 3V/m