Answer:
beat frequency = 13.87 Hz
Step-by-step explanation:
given data
lengths l = 2.00 m
linear mass density μ = 0.0065 kg/m
String A is under a tension T1 = 120.00 N
String B is under a tension T2 = 130.00 N
n = 10 mode
to find out
beat frequency
solution
we know here that length L is
L = n ×
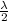 ........1
........1
so λ =
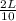
and velocity is express as
V =
 .................2
.................2
so
frequency for string A = f1 =
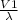
f1 =
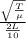
f1 =
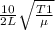
and
f2 =
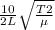
so
beat frequency is = f2 - f1
put here value
beat frequency =
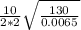 -
-
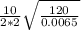
beat frequency = 13.87 Hz