Question

The digits of a two-digit number sum to 8. When the digits are reversed the resulting number is 18 less than the onginal

number. What is the original number?
​

Answer 1

53

Explanation:

Given: The sum of two digit number is 8

Reversing the digit will get us number 18 less than the original.

Lets take x as tenth digit of our number and y as unit digit of our number.

As given sum of digit is 8

∴
`x+y= 8`

∴
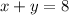
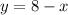`y= 8-x` - equation 1

We also know that reversing the digit will get us number 18 less than the original.

∴
`10y+x = 10x +y-18`

Now, lets put the value of y from equation 1

⇒
`10(8-x) + x = 10x+ (8-x)- 18`

⇒
`80-9x= 9x-10`

⇒
`90= 18x`

∴
`x= 5`

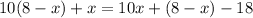
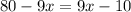
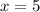
Next, substituting the value of x in equation 1

`y= 8-x`

⇒
`y= 8-5 = 3`

∴
`y= 3`

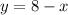
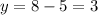
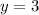
∴ The original number is 53, sum of the digit is 8 and if we reverse the digit of the number, we get 35, which is 18 less than the original number.