Question

It is weigh-in time for the local under-85-kg rugby team. The bathroom scale used toassess eligibility can be described by Hooke’s law and is depressed 0.75 cm byitsmaximum load of 120 kg. (a) What is the spring’s effective spring constant? (b) Aplayer stands on the scales and depresses it by 0.48 cm. Is he eligible to play on thisunder-85-kg team?

Answer 1

To solve this problem it is necessary to apply the equations given in Newton's second law as well as Hooke's Law.

Since Newton's second law we have that force is

F = mg

Where,

m = mass

g = gravity

From the hook law, let us know that

F = -kx

Where

k = Spring constant

x = Displacement

Re-arrange to find k,

`k = -(F)/(x)`

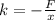
PART A ) We can replace the Newton definitions here, then

`k = -(mg)/(x)`

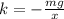
Replacing with our values we have that

`k = (120*9.8)/(-0.75*10^(-2))`

`k = 1.57*10^5N/m`

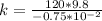
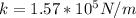
Therefore the required value of the spring constant is
`1.57*10^5N/m`

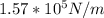
PART B) We can also equating both equation to find the mass, then

`mg = -kx`

`m = (-kx)/(g)`

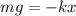
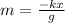
Replacing with tour values we have

`m = (1.568*10^5(-9.48*10^(-2)))/(9.8)`

`m = 76.8Kg`

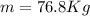
Therefore the mass of the player can be of 76.8Kg, then the player is eligible to play because the mass is less than 85Kg