Question

Determine whether the sequence converges or diverges. If it converges, find the limit. (If an answer does not exist, enter DNE.) an = 4n cos(7nπ)

Answer 1

The sequence diverges.

Explanation:

A sequence
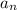`a_(n)` converges when
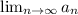`\lim_(n \rightarrow \infty) a_(n)` is a real number.

In this question, the sequence given is:

`a_(n) = 4ncos((7n\pi))`

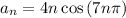
The cosine is always going to be between -1 and 1, so for the convergence of the sequence, we look it as:
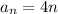`a_(n) = 4n`. So

`\lim_(n \rightarrow \infty) a_(n) = \lim_(n \rightarrow \infty) 4n = \infty`

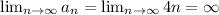
Since the limit is not a real number, the sequence diverges.