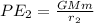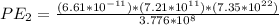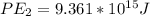Question

The volume of water in the Pacific Ocean is about 7.00 × 108 km3. The density of seawater is about 1030 kg/m3. For the sake of the calculations, treat the Pacific Ocean as a point like object (obviously a very rough approximation). 1) Determine the gravitational potential energy of the Moon–Pacific Ocean system when the Pacific is facing away from the Moon. (Express your answer to three significant figures.) Answer in Joules 2) Repeat the calculation when Earth has rotated so that the Pacific Ocean faces toward the Moon. (Express your answer to three significant figures.) Answer in Joules

Answer 1

The concepts used to solve this exercise are given through the calculation of distances (from the Moon to the earth and vice versa) as well as the gravitational potential energy.

By definition the gravitational potential energy is given by,

`PE=(GMm)/(r)`

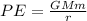
Where,

m = Mass of Moon

G = Gravitational Universal Constant

M = Mass of Ocean

r = Radius

First we calculate the mass through the ratio given by density.

`m = \rho V`

`m = (1030Kg/m^3)(7*10^8m^3)`

`m = 7.210*10^(11)Kg`

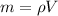
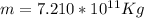
PART A) Gravitational potential energy of the Moon–Pacific Ocean system when the Pacific is facing away from the Moon

Now we define the radius at the most distant point

`r_1 = 3.84*10^8 + 6.4*10^6 = 3.904*10^8m`

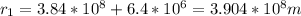
Then the potential energy at this point would be,

`PE_1 = (GMm)/(r_1)`

`PE_1 = ((6.61*10^(-11))*(7.21*10^(11))*(7.35*10^(22)))/(3.904*10^8)`

`PE_1 = 9.05*10^(15)J`

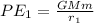
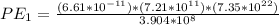
PART B) when Earth has rotated so that the Pacific Ocean faces toward the Moon.

At the nearest point we perform the same as the previous process, we calculate the radius

`r_2 = 3.84*10^8-6.4*10^6 - 3.776*10^8m`

The we calculate the Potential gravitational energy,

`PE_2 = (GMm)/(r_2)`

`PE_2 = ((6.61*10^(-11))*(7.21*10^(11))*(7.35*10^(22)))/(3.776*10^8)`

`PE_2 = 9.361*10^(15)J`