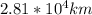Question

Suppose one of the Global Positioning System satellites has a speed of 4.46 km/s at perigee and a speed of 3.54 km/s at apogee. If the distance from the center of the Earth to the satellite at perigee is 2.23×104 km , what is the corresponding distance at apogee?

Answer 1

To solve this problem it is necessary to apply the concepts related to Kepler's second law and the conservation of angular momentum.

Kepler's second law tells us that the vector radius that unites a planet and the sun sweeps equal areas at equal times, that is, when the planet is farther from the sun, the speed at which it travels is less than when it is close to the sun.

The angular momentum is defined as

`L = m*r*v`

Where,

m= mass

r = Radius

v = Velocity

For conservation of angular momentum

`L_(apogee)=L_(perigee)`

`mv_a*r_a = mv_p*r_p`

`v_a*r_a= v_p*r_p`

`r_a = (v_p*r_p)/(v_a)`

`r_a = ((4.46)(2.23*10^4))/((3.54))`

`r_a = 2.81*10^4km`

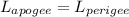
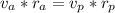
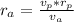
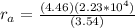
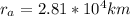
Therefore the corresponding distance at apogee is
`2.81*10^4km`