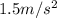Question

A solid cylinder of radius 10.0 cm rolls down an incline with slipping. The angle of the incline is 30°. The coefficient of kinetic friction on the surface is 0.400. What is the angular acceleration of the solid cylinder? What is the linear acceleration?

Answer 1

To solve this problem it is necessary to apply the expressions related to the calculation of angular acceleration in cylinders as well as the calculation of linear acceleration in these bodies.

By definition we know that the angular acceleration in a cylinder is given by

`\alpha = (2\mu_k g cos\theta)/(r)`

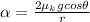
Where,

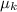`\mu_k` = Coefficient of kinetic friction

g = Gravitational acceleration

r= Radius

`\theta`= Angle of inclination

While the tangential or linear acceleration is given by,

`a = g(sin\theta-\mu_k cos\theta)`

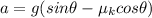
ANGULAR ACCELERATION, replacing the values that we have

`\alpha = (2\mu_k g cos\theta)/(r)`

`\alpha = (2(0.4)(9.8) cos(30))/(10*10^(-2))`

`\alpha = 67.9rad/s`

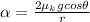
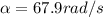
LINEAR ACCELERATION, replacing the values that we have,

`a = (9.8)(sin30-(0.4)cos(30))`

`a = 1.5m/s^2`

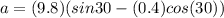
Therefore the linear acceleration of the solid cylinder is
`1.5 m/s^2`