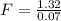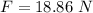Answer:
 is the final velocity of the racket.
is the final velocity of the racket.
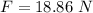
Step-by-step explanation:
Given:
- mass of the racket,

- mass of ball,

- initial speed of racket,
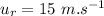
- initial speed of ball,
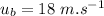
- final speed of ball,

- time of contact of racket with the ball,
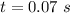
By the law of conservation of momentum:
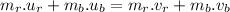
where:
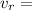 final velocity of the racket
final velocity of the racket
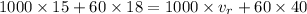
 is the final velocity of the racket.
is the final velocity of the racket.
By the Newton's second law of motion:
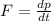 ............................(1)
............................(1)
where:
dp = change in momentum
dt = change in time
Change in momentum of ball:
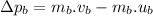

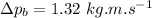
Now, using eq.(1):