Answer:
The instantaneous velocity for
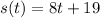 when t = 4 is
when t = 4 is
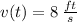 .
.
Explanation:
The average rate of change of function f over the interval is given by this expression:

The average velocity is the average rate of change of distance with respect to time

The instantaneous rate of change is defined to be the result of computing the average rate of change over smaller and smaller intervals.
The derivative of f with respect to x, is the instantaneous rate of change of f with respect to x and is thus given by the formula
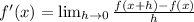
For any equation of motion s(t), we define what we call the instantaneous velocity at time t to be the limit of the average velocity, between t and t + Δt, as Δt approaches 0.
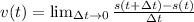
We know the equation of motion
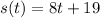 and we want to find the instantaneous velocity for the given value of t = 4.
and we want to find the instantaneous velocity for the given value of t = 4.
Applying the definition of instantaneous velocity, we get
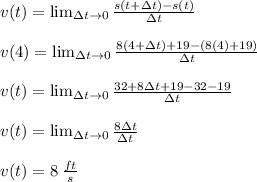
The instantaneous velocity for
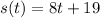 when t = 4 is
when t = 4 is
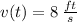 .
.