Answer:
50%
Explanation:
68-95-99.7 rule
68% of all values lie within the 1 standard deviation from mean
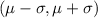
95% of all values lie within the 1 standard deviation from mean

99.7% of all values lie within the 1 standard deviation from mean
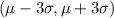
The distribution of the number of daily requests is bell-shaped and has a mean of 55 and a standard deviation of 4.
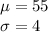
68% of all values lie within the 1 standard deviation from mean
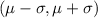 =
=
 =
=
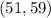
95% of all values lie within the 2 standard deviation from mean
 =
=
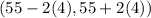 =
=
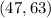
99.7% of all values lie within the 3 standard deviation from mean
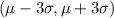 =
=
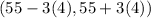 =
=
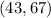
Refer the attached figure
P(43<x<55)=2.5%+13.5%+34%=50%
Hence The approximate percentage of light bulb replacement requests numbering between 43 and 55 is 50%