Question

Find the Vertex of the function glven below?
y = x^2-4x+1

Answer 1

The vertex of the function is (2, -3).

Explanation:

Given:

`y=x^(2)-4x+1`

So, to find the vertex of the function we will get the equation in the form:

`y=ax^(2) +bx+c`

`y=1x^(2)+(-4)x+1`

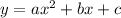
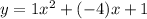
So,
`a=1,b=-4,c=1`

Then, we calculate the x-coordinate of the vertex:

`x=(-b)/(2a)`

`x=(-(-4))/(2*1)\\x=(4)/(2)`

`x=2`

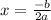
And now, we get the
`y` value of vertex of the function:

`y=1x^(2)-4x+1`

`y=1* 2^(2)+(-4)* (2)+1`

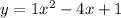
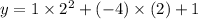
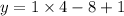`y=1* 4-8+1` (when the opposite signs multiply the result is negative)

`y=4-8+1`

`y=-3`

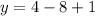
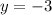
Therefore, the vertex is at
`(x,y)=(2,-3)`.