Answer:
Approximately
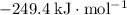 .
.
Step-by-step explanation:
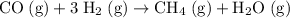 .
.
Note that hydrogen gas
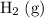 is the most stable allotrope of hydrogen. Since
is the most stable allotrope of hydrogen. Since
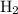 is naturally a gas under standard conditions, the standard enthalpy of formation of
is naturally a gas under standard conditions, the standard enthalpy of formation of
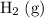 would be equal to zero. That is:
would be equal to zero. That is:
Look up the standard enthalpy of formation for the other species:
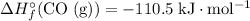 ,
,
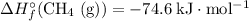 .
.
(Source: CRC Handbook of Chemistry and Physics, 84th Edition (2004).)
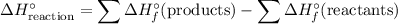 .
.
In other words, the standard enthalpy change of a reaction is equal to:
- the sum of enthalpy change of all products, minus
- the sum of enthalpy change of all reactants.
In this case,
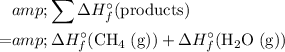 .
.
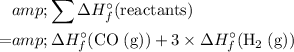 .
.
Note that the number
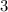 in front of
in front of
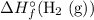 corresponds to the coefficient of
corresponds to the coefficient of
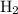 in the chemical equation.
in the chemical equation.
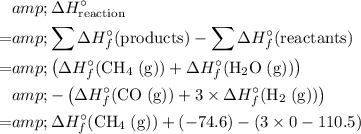 .
.
In other words,
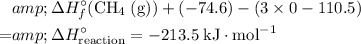 .
.
Therefore,
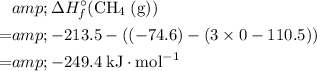 .
.