Question

The exponential model Upper A equals 104.8 e Superscript 0.001 t describes the​ population, A, of a country in​ millions, t years after 2003. Use the model to determine when the population of the country will be 106 million.

Answer 1

Answer: The population of the country will be 106 millions in 2014.

Explanation:

The exercise gives you the following exponential model, which describes the​ population "A" (in​ millions) of a country "t" years after 2003:

`A=104.8 e^(0.001 t)`

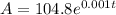
In this case you must determine when the population of that country will be 106 millions, so you can identify that:

`A=106`

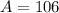
Now you need to substitute this value into the exponential model given in the exercise:

`106=104.8 e^(0.001 t)`

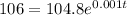
Finally, you must solve for "t", but first it is important to remember the following Properties of logarithms:

`ln(a)^b=b*ln(a)\\\\ln(e)=1`

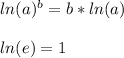
Then:

`(106)/(104.8)=e^(0.001 t)\\\\ln((106)/(104.8))=ln(e)^(0.001 t)\\\\ln((106)/(104.8))=0.001 t(1)\\\\(ln((106)/(104.8)))/(0.001)}=t\\\\t=11.38\\\\t\approx11`

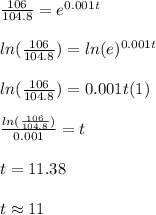
Notice that in 11 years the population will be 106 millions, then the year will be:

`2003+11=2014`

The population of the country will be 106 millions in 2014.