Question

Suppose that we are testing a coin to see if it is fair, so our hypotheses are: H0: p = 0.5 vs Ha: p ≠ 0.5. In each of (a) and (b) below, use the "Edit Data" option on StatKey to find the p-value for the sample results and give a conclusion in the test. a. We get 56 heads out of 100 tosses. b. We get 560 heads out of 1000 tosses. c. Compare the sample proportions in parts (a) and (b). Compare the p-values. Why are the p-values so different?

Answer 1

`H_0: p = 0.5\\H_a: p \\eq 0.5`

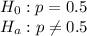
a. We get 56 heads out of 100 tosses.

We will use one sample proportion test

x = 56

n = 100

`\widehat{p}=(x)/(n)`

`\widehat{p}=(56)/(100)`

`\widehat{p}=0.56`

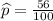
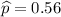
Formula of test statistic =
`\frac{\widehat{p}-p}{\sqrt{(p(1-p))/(n)}}`

=
`\frac{0.56-0.5}{\sqrt{(0.5(1-0.5))/(100)}}`

=
`1.2`

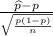
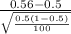
refer the z table for p value

p value = 0.8849

a. We get 560 heads out of 1000 tosses.

We will use one sample proportion test

x = 560

n = 1000

`\widehat{p}=(x)/(n)`

`\widehat{p}=(560)/(1000)`

`\widehat{p}=0.56`

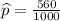
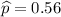
Formula of test statistic =
`\frac{\widehat{p}-p}{\sqrt{(p(1-p))/(n)}}`

=
`\frac{0.56-0.5}{\sqrt{(0.5(1-0.5))/(1000)}}`

=
`3.794`

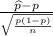
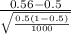
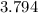
refer the z table for p value

p value = .000148

p value of part B is less than Part A because part B have 10 times the number the tosses.