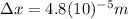Question

You apply forces of magnitude 4.2×104N to the top and bottom surfaces of a brass cube. The forces are tangent to each surface and parallel to the sides of each surface. If the cube is 2.5 cm on a side, what is the resulting shear displacement? The shear modulus for brass is 3.5×1010Pa.

Answer 1

Answer:
`4.8(10)^(-5) m`

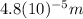
Step-by-step explanation:

We can solve this problem by the following equation:

`\eta=(F.h)/(A \Delta x)`

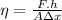
Where:

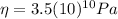`\eta=3.5(10)^(10)Pa` is the shear modulus for brass

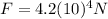`F=4.2(10)^(4)N` is the applied force

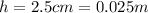`h=2.5 cm=0.025 m` is the height of the cube

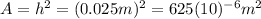`A=h^(2)=(0.025 m)^(2)=625(10)^(-6) m^(2)` is the area of each surface of the cube

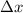`\Delta x` is the shear displacement

Finding
`\Delta x`:

`\Delta x=(F.h)/(A \eta)`

`\Delta x=((4.2(10)^(4)N)(0.025 m))/((625(10)^(-6) m^(2))(3.5(10)^(10)Pa))`

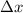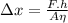
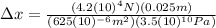
Finally:

`\Delta x= 4.8(10)^(-5) m`