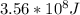Question

One at your summer lunar space camp activities is to launch n 1170-kg rocket from the surface of the Moon. You are a serious space camper and you launch a serious rocket: II reaches an altitude of 211 km. What gain m gravitational potential memo does the launch accomplish? The mass and radios of the Moon are 7.36 x 10^22 kg and 1740 km, respectively.

Answer 1

To solve this problem it is necessary to apply the concepts related to gravitational potential energy.

The change in gravitational potential energy is given by,

`\Delta PE = PE_f - PE_i`

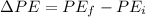
Where,

`PE = (GMm)/(R)`

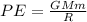
Here,

G = Gravitational Universal Constant

M = Mass of Earth

m = Mass of Object

R = Radius

Replacing we have that

`\Delta PE = (GMm)/(R+h) -(GMm)/(R)`

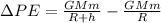
Note that h is the height for this object. Then replacing with our values we have,

`\Delta PE = (GMm)/(R+h) -(GMm)/(R)`

`\Delta PE = GMm((1)/(R) -(1)/(R+h))`

`\Delta PE = (6.65*10^(-11))(7.36*10^(22))(1170)((1)/(1740*10^3) -(1)/(211*10^3+1740*10^3))`

`\Delta PE = 57264.48*10^(11)(5.1255*10^(-7)-5.747*10^(-7))`

`\Delta PE = 3.56*10^8J`

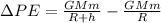
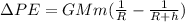
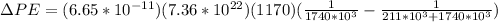
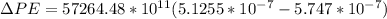
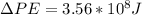
Therefore the gravitational potential is
`3.56*10^8J`