Question

In 2010, a town's population was 83 thousand. By 2015 the population had grown to 105 thousand.a) Find an exponential equation for the town's population.b) Determine in what year the population will exceed 135 thousand. As always, show your work for finding the equation and solving for the year algebraically.

Answer 1

(a)
`y = 83 (1.048)^x`

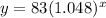
(b) 2020

Explanation:

(a) Let the exponential equation that shows the population in thousand after x years,

`y = ab^x`

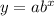
Also, suppose the population is estimated since 2010,

So, x = 0, y = 83 thousands,

`83 = ab^0`

`\implies a = 83`

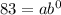
Again by 2015 the population had grown to 105 thousand,

i.e. y = 105, if x = 5,

`\implies 105 = ab^5`

`\implies 105 = 83 b^5`

`\implies b = ((105)/(83))^(1)/(5)=1.0481471103\approx 1.048`

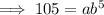
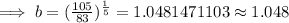
Hence, the required function,

`y = 83 (1.048)^x`

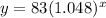
(b) if y = 135,

`135 = 83(1.048)^x`

`\implies x = 10.375\approx 10`

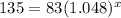
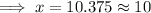
Hence, after approximately 10 years since 2010 i.e. in 2020 the population would be 135.