Question

The energy levels of a particular quantum object are -11.7 eV, -4.2 eV, and -3.3 eV. If a collection of these objects is bombarded by an electron beam so that there are some objects in each excited state, what are the energies of the photons that will be emitted?

Answer 1

To solve this problem it is necessary to apply an energy balance equation in each of the states to assess what their respective relationship is.

By definition the energy balance is simply given by the change between the two states:

`|\Delta E_(ij)| = |E_i-E_j|`

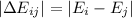
Our states are given by

`E_1 = -11.7eV`

`E_2 = -4.2eV`

`E_3 = -3.3eV`

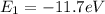
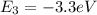
In this way the energy balance for the states would be given by,

`|\Delta E_(12)| = |E_1-E_2|\\|\Delta E_(12)| = |-11.7-(-4.2)|\\|\Delta E_(12)| = 7.5eV\\`

`|\Delta E_(13)| = |E_1-E_3|\\|\Delta E_(13)| = |-11.7-(-3.3)|\\|\Delta E_(13)| = 8.4eV`

`|\Delta E_(23)| = |E_2-E_3|\\|\Delta E_(23)| = |-4.2-(-3.3)|\\|\Delta E_(23)| = 0.9eV`

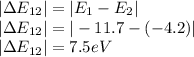
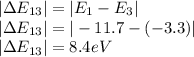
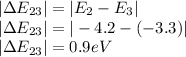
Therefore the states of energy would be

Lowest : 0.9eV

Middle :7.5eV

Highest: 8.4eV