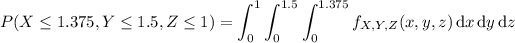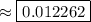a.
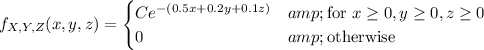
is a proper joint density function if, over its support,
 is non-negative and the integral of
is non-negative and the integral of
 is 1. The first condition is easily met as long as
is 1. The first condition is easily met as long as
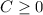 . To meet the second condition, we require
. To meet the second condition, we require
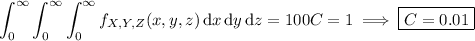
b. Find the marginal joint density of
 and
and
 by integrating the joint density with respect to
by integrating the joint density with respect to
 :
:
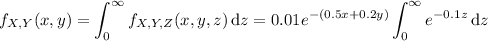
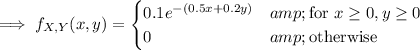
Then
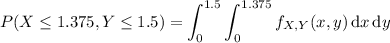
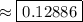
c. This probability can be found by simply integrating the joint density: