Question

Tanya prepared 4 different letters to be sent to 4 different addresses. For each letter, she prepared an envelope with its correct address. If the 4 letters are to be put into the 4 envelopes at random, what is the probability that only 1 letter will be put into the envelope with its correct address?

A. 1/24
B. 1/8
C. 1/4
D. 1/3
E. 3/8

Answer 1

The probability that only 1 letter will be put into the envelope with its correct address is
`(1)/(3)`

Explanation:

Given:

Number of Letters=4

Number of addresses= 4

To Find:

The probability that only 1 letter will be put into the envelope with its correct address=?

Solution:

Let us assume first letter goes in correct envelope and others go in wrong envelopes, then

=> Probability putting the first letter in correct envelope =
`(1)/(4)`

=> Probability putting the second letter in correct envelope =
`(2)/(3)`

=> Probability putting the third letter in correct envelope=
`(1)/(2)`

=> Probability putting the fourth letter in correct envelope = 1;

( only 1 wrong addressed envelope is left);

This event can occur with other 3 envelopes too.

Hence total prob. =
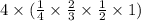
`4*((1)/(4)*(2)/(3)*(1)/(2)*1)`

=>
`(1)/(3)`