Question

A cannon fires a cannonball of mass 16.0 kg by applying a force of 2750 N along the 1.25 m length of the barrel. (a) How much work does the cannon do on the cannonball? (b) The cannon is aimed at a 25.0° angle above the horizontal. Assume gravity is the only other force acting on the cannonball as it moves through the cannon barrel. (That is, ignore all frictional forces.) What is the net work done by these 2 forces on the cannonball while it is in the cannon barrel?

Answer 1

To develop this problem it is necessary to apply the concepts related to Work and energy conservation.

By definition we know that the work done by a particle is subject to the force and distance traveled. That is to say,

`W = F*d`

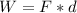
Where,

F= Force

d = Distance

On the other hand we know that the potential energy of a body is given based on height and weight, that is

`PE = -mgh`

The total work done would be given by the conservation and sum of these energies, that is to say

`W_(net) = W+PE`

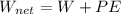
PART A) Applying the work formula,

`W = F*d\\W = 2750*1.25\\W = 3437.5J`

PART B) Applying the height equation and considering that there is an angle in the distance of 25 degrees and the component we are interested in is the vertical, then

`PE = -mgh*sin25`

`PE = -16*9.81*1.15sin25`

`PE = -82.9J`

The net work would then be given by

`W_(net) = W+PE`

`W_(net) = 3437.5J-82.9J`

`W_(net) = 3354.6J`

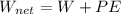
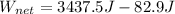
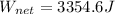
Therefore the net work done by these 2 forces on the cannonball while it is in the cannon barrel is 3355J