Answer:
The type of sequence. 4,9,13,22 is neither arithmetic nor geometric
Step-by-step explanation:
For arithmetic progression:
Formula used = a +(n-1)d
Where d is the difference of numbers in the sequence =
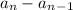
Hence,
=

= 9-4 = 5
=

= 13 – 9 = 4
Since the common difference is not same
Hence it is not arithmetic
For geometric progression:
Formula used =
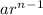
Where r is the common ratio of terms=
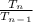
=
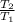
= 9/4
Similarly,
=
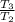
=13/9
Since the common ratio is not same
Hence it is not a geometric