Answer:
B.
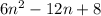
Explanation:
Given,
The number of smaller cubes =
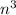
So, the number of cubes that have no coloured faces. =
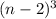 ,
,
Note : If a cube painted outside having side n is split into n³ cubes, then the volume volume that is not painted = (n-2)³
Thus, the remaining cubes that have been painted red on at least one of their faces
= Total cubes - cubes with no painted face
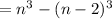
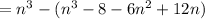
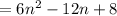
Hence, OPTION B is correct.