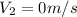Question

A body is traveling at 5.0 m/s along the positive direction of an x axis; no net force acts on the body. An internal explosion separates the body into two parts, each of mass 4 kg, and increases the total kinetic energy by 100 J. The forward part continues to move in the original direction of motion. (a) What is the speed of the rear part? (b) What is the speed of the forward part?

Answer 1

To solve this problem it is necessary to apply the concepts related to the conservation of momentum and conservation of kinetic energy.

By definition kinetic energy is defined as

`KE = (1)/(2) mv^2`

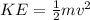
Where,

m = Mass

v = Velocity

On the other hand we have the conservation of the moment, which for this case would be defined as

`m*V_i = m_1V_1+m_2V_2`

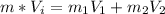
Here,

m = Total mass (8Kg at this case)

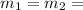`m_1=m_2 =` Mass each part

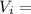`V_i =` Initial velocity

`V_2 =` Final velocity particle 2

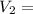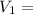`V_1 =` Final velocity particle 1

The initial kinetic energy would be given by,

`KE_i=(1)/(2)mv^2`

`KE_i = (1)/(2)8*5^2`

`KE_i = 100J`

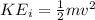
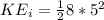
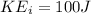
In the end the energy increased 100J, that is,

`KE_f = KE_i KE_(increased)`

`KE_f = 100+100 = 200J`

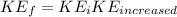
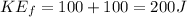
By conservation of the moment then,

`m*V_i = m_1V_1+m_2V_2`

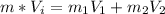
Replacing we have,

`(8)*5 = 4*V_1+4*V_2`

`40 = 4(V_1+V_2)`

`V_1+V_2 = 10`

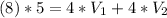
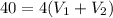
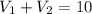
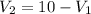`V_2 = 10-V_1`(1)

In the final point the cinematic energy of EACH particle would be given by

`KE_f = (1)/(2)mv^2`

`KE_f = (1)/(2)4*(V_1^2+V_2^2)`

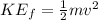
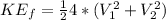
`200J=(1)/(2)4*(V_1^2+V_2^2)`(2)

So we have a system of 2x2 equations

`V_2 = 10-V_1`

`200J=(1)/(2)4*(V_1^2+V_2^2)`

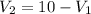
Replacing (1) in (2) and solving we have to,

200J=\frac{1}{2}4*(V_1^2+(10-V_1)^2)

PART A:
`V_1 = 10m/s`

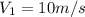
Then replacing in (1) we have that

PART B:
`V_2 = 0m/s`