Question

Evaluate
`\frac{\sqrt[4]{9}\sqrt[2]{9} }{\sqrt[4]{9^(5) } }`

Answer 1

1/3 is simplified form of given expression.

Explanation:

Given that:

=
`\sqrt[4]{9} \sqrt[2]{9}/ \sqrt[4]{9^5}`

Now we will write the radical in simple form first:

=
`9^(1/4) * 9^(1/2)/ 9^(5/4)`

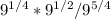
As bases are same, powers will be added and subtracted as follows:

=
`9^(1/4 + 1/2 - 5/4)`

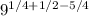
By simplifying the powers:

=
`9^(5/20 + 10/20 - 25/20)`

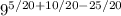
Now denominators are same so numerators can be added

=
`9^(-10/20)\\= 9^(-1/2)`

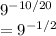
For removing the negative sign the base will be inverted:

=
`(1/9)^(1/2)`

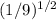
This can be written as follows:

=
`√(1/9) \\= 1/3`

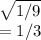
i hope it will help you!