The amount of money invested in 11% account is $10000
Solution:
Given that, A bank customer invests a total of $7000in two savings accounts.
One account yields 10% simple interest and the other 11% simple interest.
The customer earned a total of $800interest for the year.
Now, let the amount invested in 11% account be $n, then amount in other account will be 7000 – n
The simple interest is given as:
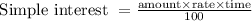
Then, for 10% account:

And for 11% account:

Now, we know that, total simple interest = S.I from 10% account + S.I from 11% account
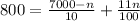
80000 = 10(7000 - n) + 11n
80000 = 70000 – 10n + 11n
11n – 10n = 80000 – 70000
n = 10000
Hence, the amount of money invested in 11% account is $10000