Answer:
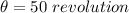
Step-by-step explanation:
It is given that,
Mass of the grindstone, m = 3 kg
Radius of the grindstone, r = 8 cm = 0.08 m
Initial speed of the grindstone,
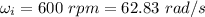
Finally it shuts off,

Time taken, t = 10 s
Let
 is the angular acceleration of the grindstone. Using the formula of rotational kinematics as :
is the angular acceleration of the grindstone. Using the formula of rotational kinematics as :
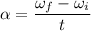
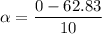
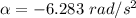
Let
 is the number of revolutions of the grindstone after the power is shut off. Now using the third equation of rotational kinematics as :
is the number of revolutions of the grindstone after the power is shut off. Now using the third equation of rotational kinematics as :
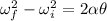
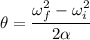
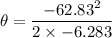
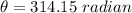

or
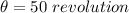
So, the number of revolutions of the grindstone after the power is shut off is 50.