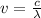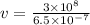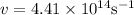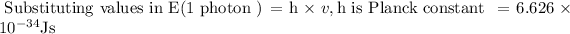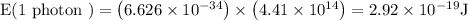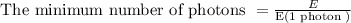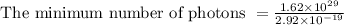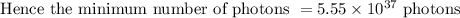Question

The net change in the multistep biochemical process of photosynthesis is that CO2 and H2O form glucose (C6H12O6) and O2. Chlorophyll absorbs light in the 600 to 700 nm region.

(a) Write a balanced thermochemical equation for formation of 1.00 mol of glucose

(b) What is the minimum number of photons with λ = 680. nm needed to prepare 1.00 mol of glucose?

Answer 1

(a)The balanced thermochemical equation for formation of 1.00 mol of glucose is:
`6 \mathrm{CO}_(2)+6 \mathrm{H}_(2) \mathrm{O} \longrightarrow \mathrm{C}_(6) \mathrm{H}_(12) \mathrm{O}_(6)+6 \mathrm{O}_(2)`

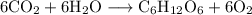
(b) The minimum number of photons with λ = 680 nm needed to prepare 1.00 mol of glucose is
`5.55 * 10^(37) \text { photons }`

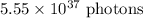
Step-by-step explanation:

(a) Both side of reaction have equal number of elements therefore number of reactant is equal to number of product hence following balanced equation is achieved :
`6 \mathrm{CO}_(2)+6 \mathrm{H}_(2) \mathrm{O} \longrightarrow \mathrm{C}_(6) \mathrm{H}_(12) \mathrm{O}_(6)+6 \mathrm{O}_(2)`

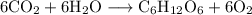
(b) According to theory of special relativity which expresses fact in equation about mass and energy is:
`\mathbf{E}=\mathbf{m} \mathbf{c}^(2) \text { and here } \mathrm{c}^(2) \text { is speed of light }`

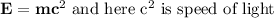
Here λ = 680 nm,

`\mathrm{n}\left(\mathrm{C}_(6) \mathrm{H}_(12) \mathrm{O}_(6)\right)=1 \mathrm{mol}`

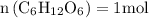
Molar mass of glucose = 180.156 g/mol

`\text { Therefore } m=180.156 \mathrm{g}, \mathrm{c}=3 * 10^(8)`

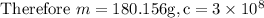
Substituting values in above equation

`\mathrm{E}=180.156 *\left(3 * 10^(8)\right)^(2)=1.62 * 10^(29) \mathrm{J}`

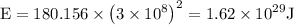
Hence it is known that

E (1 photon) = h × v

`v=(c)/(\lambda)`

`v=(3 * 10^(8))/(6.5 * 10^(-7))`

`v=4.41 * 10^(14) \mathrm{s}^(-1)`

`\text { Substituting values in } \mathrm{E}(1 \text { photon })=\mathrm{h} * v, \mathrm{h} \text { is Planck constant }=6.626 * 10^(-34) \mathrm{J} \mathrm{s}`

`\mathrm{E}(1 \text { photon })=\left(6.626 * 10^(-34)\right) *\left(4.41 * 10^(14)\right)=2.92 * 10^(-19) \mathrm{J}`

`\text { The minimum number of photons }=\frac{E}{\mathrm{E}(1 \text { photon })}`

`\text { The minimum number of photons }=(1.62 * 10^(29))/(2.92 * 10^(-19))`

`\text { Hence the minimum number of photons }=5.55 * 10^(37) \text { photons }`