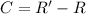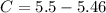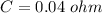Answer:
a) Approximate the change in R is 0.5 ohm.
b) The actual change in R is 0.04 ohm.
Explanation:
Given : The total resistance R of two resistors connected in parallel circuit is given by
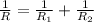
To find :
a) Approximate the change in R ?
b) Compute the actual change.
Solution :
a) Approximate the change in R
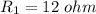 and
and
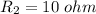
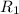 is decreased from 12 ohms to 11 ohms.
is decreased from 12 ohms to 11 ohms.
i.e.
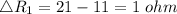
 is increased from 10 ohms to 11 ohms.
is increased from 10 ohms to 11 ohms.
i.e.

The change in R is given by,
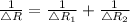
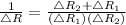
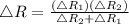
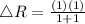

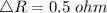
b) The actual change in Resistance
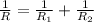
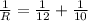
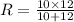
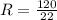
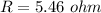
When resistances are charged,
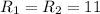
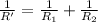
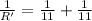
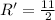

Change in resistance is given by,